SAT collision detection polygon and cicle

I got inspirited for writing this post because of my youtube video in which I show a demonstration of separating axis theorem. In the video, I show tree types of collision: polygon – polygon, circle – circle, and lastly the most tricky on polygon – circle. The video doesn’t even have at the time writing this post over 100 views but it has got comments about how I do it. So that’s what this post will be about.

I’ll say at this point of writing I’ll not provide any code examples on this one and I’ll only show direction how you could solve the problem. I expect you to already understand separating axis theorem. Also, you should have made already polygon – polygon, circle – circle detection to move on this one. Reason for this is because I worked about three years ago last time with SAT and I’m lazy to write example code which features SAT.

I’ll first tell about how things were when I faced this problem. I could find good tutorials relating to SAT and I did pretty easily implement it after following them. And when it was time for polygon – circle suddenly I was unable to find anything. So long story short: I just figured it out and it did turn out pretty easily.

Ok now let’s get into the point. Let’s think about what we are doing when we check collision polygon against polygon. We project the edges and then check is here overlappings. And the circle doesn’t have edges like polygon has, right? Well, that’s usually the case but what about if we calculated edges for circle in relation to polygons edges?

See the example below where I have calculated edge for the circle in relation to points B and C.

Yet another example with a different edge.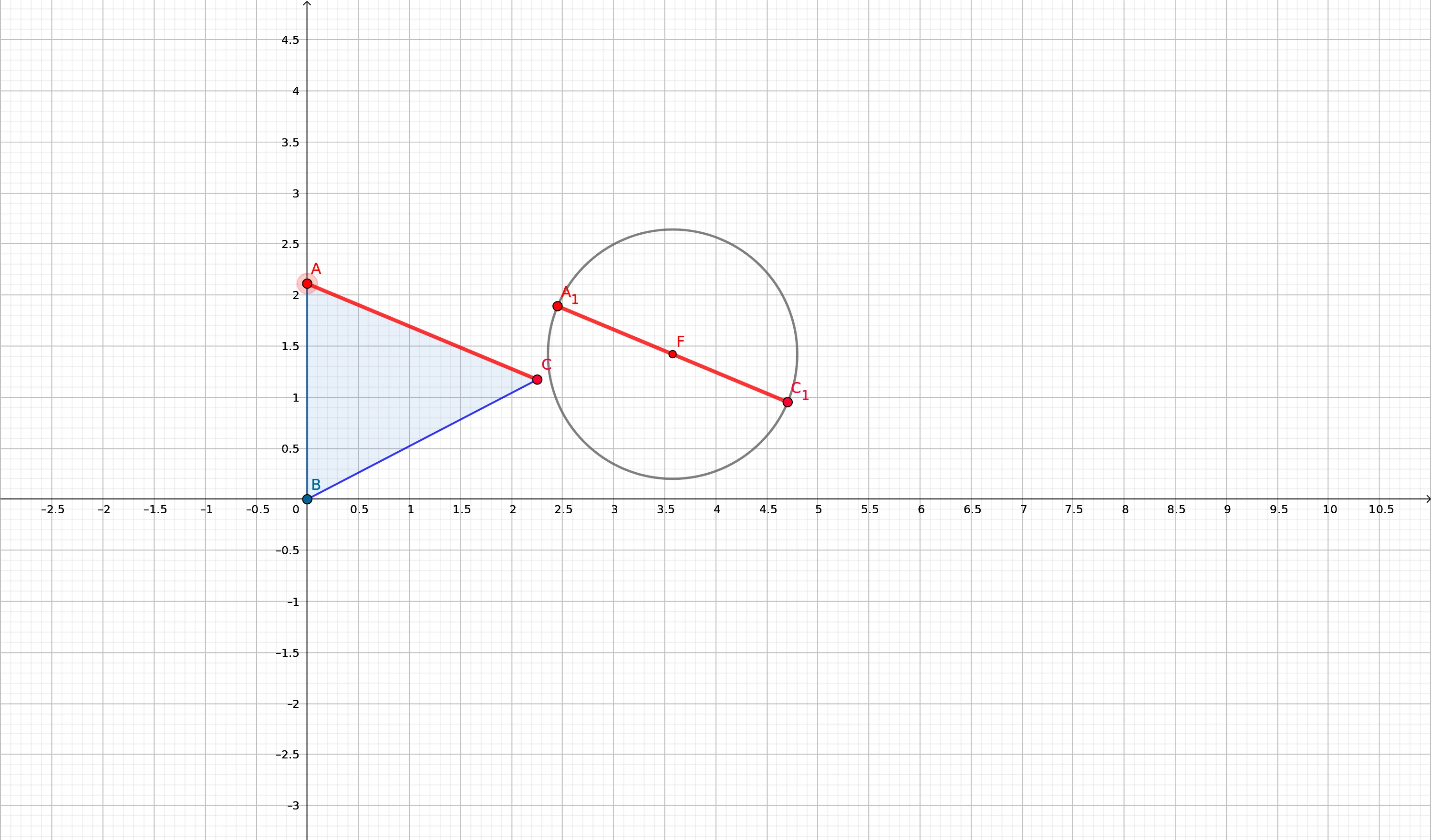

Basically how this is done is not very complicated. So let’s think about what we know already about the objects. We know positions of the triangle’s points and circle’s position as well radius. First thing what we should calculate is the angle between points B and C. This can be done with the following equation in python:

math.atan2(c.x - b.x , c.y - b.y)

# Or if you want the answer in degrees:
math.atan2(c.x - b.x , c.y - b.y) * 180 / math.pi

When we have the angle we can now easily calculate points B1 and C1 using point F, circle’s radius and the angle we just calculated. In other words, we’ll calculate endpoint for vector. This could be done with the following equation:

x = center.x + radius * math.cos(angle);
y = center.y + radius * math.sin(angle);

# In degrees
x = center.x + radius * math.cos((math.pi * angle) / 180);
y = center.y + radius * math.sin((math.pi * angle) / 180);

Next, you can do the projection as you could do with polygon – polygon! Now just iterate over all edges and do the same steps. Hopefully this post helped at least someone.